ę╗Īó▓╗Ą╚ĻP(gu©Īn)ŽĄ├„’@ą═
┤╦ŅÉå¢(w©©n)Ņ}Ą─╠ž³c(di©Żn)╩Ūį┌Ņ}─┐ųąĢ■(hu©¼)│÷¼F(xi©żn)├„’@Ą─▒Ē╩Š▓╗Ą╚ĻP(gu©Īn)ŽĄĄ─ĻP(gu©Īn)µIūųŻ¼╚ń“┤¾ė┌”���Īó“ąĪė┌”�����Īó“▓╗─▄│¼▀^(gu©░)”����Īó“▓╗╔┘ė┌”��Īó“ūŅČÓ”Ą╚�ĪŻ
└²1 (╣■Ā¢×I╩ą)ļp╚žĘ■čbĄĻ└Ž░ÕĄĮÅS╝ę▀x┘Å(g©░u)AĪóBā╔ĘNą═╠¢(h©żo)Ą─Ę■čbŻ¼╚¶õN╩█ę╗╝■Aą═Ę■čb┐╔½@└¹18į¬�Ż¼õN╩█ę╗╝■Bą═Ę■čb┐╔½@└¹30į¬Ż¼Ė∙ō■(j©┤)╩ął÷(ch©Żng)ąĶŪ¾�����Ż¼Ę■čbĄĻ└Ž░ÕøQČ©�����Ż¼┘Å(g©░u)▀M(j©¼n)Aą═Ę■čbĄ─öĄ(sh©┤)┴┐ę¬▒╚┘Å(g©░u)▀M(j©¼n)Bą═Ę■čböĄ(sh©┤)┴┐Ą─2▒Č▀ĆČÓ4╝■����Ż¼ŪęAą═Ę■čbūŅČÓ┐╔┘Å(g©░u)▀M(j©¼n)28╝■Ż¼▀@śėĘ■čb╚½▓┐╩█│÷║¾���Ż¼┐╔╩╣┐é½@└¹▓╗╔┘ė┌699į¬����Ż¼å¢(w©©n)ėąÄūĘN▀M(j©¼n)žøĘĮ░Ė?╚ń║╬▀M(j©¼n)žø?
Ęų╬÷Ż║ė╔Ņ}ęŌ����Ż¼▒ŠŅ}▓╗Ą╚ĻP(gu©Īn)ŽĄĘŪ│Ż├„’@Ż¼ė╔ā╔éĆ(g©©)▒Ē╩Š▓╗Ą╚ĻP(gu©Īn)ŽĄĄ─ĻP(gu©Īn)µIūų╝┤┐╔┐┤│÷�����Ż¼╝┤“ūŅČÓ”║═“▓╗╔┘ė┌”Ż¼ę“┤╦ę¬ĮŌøQ▒ŠŅ}╬ęéā┐╔ęįų▒ĮėĖ∙ō■(j©┤)▀@ā╔éĆ(g©©)ĻP(gu©Īn)µIūų┴ą│÷▓╗Ą╚╩ĮĮM���ĪŻ
ĮŌŻ║įO(sh©©)Bą═Ę■čb┘Å(g©░u)▀M(j©¼n)x╝■Ż¼ätAą═Ę■čb┘Å(g©░u)▀M(j©¼n)╝■����Ż¼Ė∙ō■(j©┤)Ņ}ęŌŻ¼Ą├

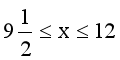
ĮŌĄ├
ę“?y©żn)ķx×ķš¹öĄ(sh©┤)��Ż¼╦∙ęįx=10�����Īó11���Īó12
╦∙ęį�����Īó26����Īó28
╦∙ęįėą╚²ĘN▀M(j©¼n)žøĘĮ░ĖŻ║Bą═Ę■čb┘Å(g©░u)▀M(j©¼n)10╝■Ż¼Aą═Ę■čb┘Å(g©░u)▀M(j©¼n)24╝■╗“Bą═Ę■čb┘Å(g©░u)▀M(j©¼n)11╝■����Ż¼Aą═Ę■čb┘Å(g©░u)▀M(j©¼n)26╝■;Bą═Ę■čb┘Å(g©░u)▀M(j©¼n)12╝■Ż¼Aą═Ę■čb┘Å(g©░u)▀M(j©¼n)28╝■�����ĪŻ
└²2 (▀BįŲĖ█╩ą)╣Ō├„▐r(n©«ng)ł÷(ch©Żng)ėą─│ĘNų▓╬’10000Ū¦┐╦�����Ż¼┤“╦Ń╚½▓┐ė├ė┌╔·«a(ch©Żn)Ė▀┐Ų╝╝╦ÄŲĘ║═▒ŻĮĪ╩│ŲĘ�ĪŻ╚¶╔·«a(ch©Żn)Ė▀┐Ų╝╝╦ÄŲĘŻ¼1Ū¦┐╦įōų▓╬’┐╔╠ߤÆ│÷0.01Ū¦┐╦Ą─Ė▀┐Ų╝╝╦ÄŲĘ����Ż¼īó«a(ch©Żn)╔·╬█╚Š╬’0.1Ū¦┐╦Ż¼├┐1Ū¦┐╦Ė▀┐Ų╝╝╦ÄŲĘ┐╔½@└¹ØÖ(r©┤n)5000į¬;├┐╔·«a(ch©Żn)1Ū¦┐╦▒ŻĮĪ╩│ŲĘ┐╔½@└¹ØÖ(r©┤n)100į¬���ĪŻ1Ū¦┐╦įōų▓╬’┐╔╔·«a(ch©Żn)0.2Ū¦┐╦▒ŻĮĪ╩│ŲĘ����Ż¼īó«a(ch©Żn)╔·╬█╚Š╬’0.04Ū¦┐╦�����ĪŻę¬╩╣┐é└¹ØÖ(r©┤n)▓╗Ą═ė┌410000į¬Ż¼╦∙«a(ch©Żn)╔·Ą─╬█╚Š╬’┐é┴┐▓╗│¼▀^(gu©░)880Ū¦┐╦���Ż¼Ū¾ė├ė┌╔·«a(ch©Żn)Ė▀┐Ų╝╝╦ÄŲĘĄ─įōų▓╬’ųž┴┐Ą─ĘČć·��ĪŻ
Ęų╬÷Ż║ė╔Ņ}ęŌ║▄╚▌ęū░l(f©Ī)¼F(xi©żn)¾w¼F(xi©żn)▒ŠŅ}▓╗Ą╚ĻP(gu©Īn)ŽĄĄ─ā╔éĆ(g©©)ĻP(gu©Īn)µIūų�Ż¼╝┤“▓╗Ą═ė┌”║═“▓╗│¼▀^(gu©░)”�����Ż¼ę“┤╦╬ęéāŠ═Ė∙ō■(j©┤)▀@ā╔éĆ(g©©)ĻP(gu©Īn)µIūų┴ą│÷▓╗Ą╚╩ĮĮM░čå¢(w©©n)Ņ}ĮŌøQ���ĪŻ
ĮŌŻ║įO(sh©©)ė├ė┌╔·«a(ch©Żn)Ė▀┐Ų╝╝╦ÄŲĘĄ─įōų▓╬’ųž┴┐×ķxŪ¦┐╦Ż¼ätė├ė┌╔·«a(ch©Żn)▒ŻĮĪ╩│ŲĘĄ─įōų▓╬’ųž┴┐×ķ(10000-x)Ū¦┐╦����Ż¼Ė∙ō■(j©┤)Ņ}ęŌŻ¼Ą├

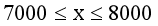
ĮŌĄ├
╦∙ęįė├ė┌╔·«a(ch©Żn)Ė▀┐Ų╝╝╦ÄŲĘĄ─įōų▓╬’ųž┴┐▓╗Ą═ė┌7000Ū¦┐╦Ūę▓╗Ė▀ė┌8000Ū¦┐╦�����ĪŻ
Č■��Īó▓╗Ą╚ĻP(gu©Īn)ŽĄļ[║¼ą═
┤╦ŅÉå¢(w©©n)Ņ}Ą─╠ž³c(di©Żn)╩ŪŅ}─┐ųąø](m©”i)ėą│÷¼F(xi©żn)▒Ē╩Š▓╗Ą╚ĻP(gu©Īn)ŽĄĄ─ĻP(gu©Īn)µIūųŻ¼ę“┤╦▓╗Ą╚ĻP(gu©Īn)ŽĄ▒╚▌^║¼ąŅ�����Ż¼ąĶę¬╬ęéāÅ─Ņ}ęŌųąĘų╬÷Ą├ĄĮ�����ĪŻ
└²3 (ÅV¢|╩Ī├»├¹╩ą)Į±─Ļ6į┬Ę▌�Ż¼╬ę╩ą─│╣¹▐r(n©«ng)╩š½@└¾ų”30揯¼ŽŃĮČ13ćŹ��Ż¼¼F(xi©żn)ėŗ(j©¼)äØūŌė├╝ū����Īóęęā╔ĘNžø▄ć╣▓10▌vŻ¼īó▀@┼·╦«╣¹╚½▓┐▀\(y©┤n)═∙╔Ņ█┌��Ż¼ęčų¬╝ūĘNžø▄ć┐╔čb└¾ų”4ćŹ║═ŽŃĮČ1ćŹ���Ż¼ęęĘNžø▄ć┐╔čb└¾ų”�����ĪóŽŃĮČĖ„2ćŹ�����ĪŻ
(1)įō╣¹▐r(n©«ng)░▓┼┼╝ū����Īóęęā╔ĘNžø▄ćĢr(sh©¬)ėąÄūĘNĘĮ░Ė?šł(q©½ng)─ŃÄ═ų·įO(sh©©)ėŗ(j©¼)│÷üĒ(l©ói)ĪŻ
(2)╚¶╝ūĘNžø▄ć├┐▌vę¬ĖČ▀\(y©┤n)▌ö┘M(f©©i)2000į¬���Ż¼ęęĘNžø▄ć├┐▌vę¬ĖČ▀\(y©┤n)▌ö┘M(f©©i)1300į¬����Ż¼ätįō╣¹▐r(n©«ng)æ¬(y©®ng)▀xō±──ĘNĘĮ░Ė╩╣▀\(y©┤n)▌ö┘M(f©©i)ūŅ╔┘?ūŅ╔┘▀\(y©┤n)▌ö┘M(f©©i)╩ŪČÓ╔┘?
Ęų╬÷Ż║▒ŠŅ}ø](m©”i)ėą├„’@Ą─▓╗Ą╚ĻP(gu©Īn)ŽĄ��Ż¼Ą½╩ŪÅ─Ņ}ęŌ┐╔ų¬▒ŠŅ}╩Ūę╗éĆ(g©©)ūŅā×(y©Łu)ĘĮ░ĖįO(sh©©)ėŗ(j©¼)å¢(w©©n)Ņ}��Ż¼ę“┤╦┐╔ęįĮ©┴ó▓╗Ą╚╩ĮĮM─Żą═üĒ(l©ói)ĮŌøQå¢(w©©n)Ņ}��ĪŻė╔Ņ}ęŌ�����Ż¼▒ŠŅ}Ą─▓╗Ą╚ĻP(gu©Īn)ŽĄ×ķŻ║10▌v╝ū�Īóęęā╔ĘNžø▄ćĄ─▀\(y©┤n)žø┐é┴┐ų┴╔┘ę¬▀_(d©ó)ĄĮ30ćŹ└¾ų”�����Ż¼13揎ŃĮČĪŻ
ĮŌŻ║(1)įO(sh©©)░▓┼┼╝ūĘNžø▄ćx▌v����Ż¼ät░▓┼┼ęęĘNžø▄ć(10-x)▌vŻ¼Ė∙ō■(j©┤)Ņ}ęŌ�Ż¼┐╔Ą├
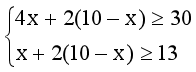
ĮŌĄ├5ąĪė┌Ą╚ė┌X┤¾ė┌Ą╚ė┌7
ę“?y©żn)ķx×ķš¹öĄ(sh©┤)Ż¼╦∙ęįx=5��Īó6��Īó7���Ż¼
╦∙ęį5�Īó4�Īó3ĪŻ
╦∙ęį▄ć▌v░▓┼┼ėą╚²ĘNĘĮ░ĖŻ║
ĘĮ░Ėę╗Ż║╝ūĘN▄ć�ĪóęęĘN▄ćĖ„5▌v;
ĘĮ░ĖČ■Ż║╝ūĘN▄ć6▌vĪóęęĘN▄ć4▌v;
ĘĮ░Ė╚²Ż║╝ūĘN▄ć7▌v�����ĪóęęĘN▄ć3▌v����ĪŻ
(2)ĘĮ░Ėę╗���Ż¼ę¬▀\(y©┤n)▌ö┘M(f©©i)Ż║
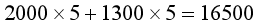
į¬
ĘĮ░ĖČ■Ż¼ę¬▀\(y©┤n)▌ö┘M(f©©i)Ż║
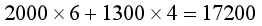
į¬
ĘĮ░Ė╚²���Ż¼ę¬▀\(y©┤n)▌ö┘M(f©©i)
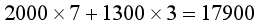
į¬
▀@šf(shu©Ł)├„�����Ż¼ĘĮ░Ėę╗╦∙ąĶ▀\(y©┤n)▌ö┘M(f©©i)ūŅ╔┘����Ż¼×ķ16500į¬�ĪŻ
└²4 (│Żų▌╩ą)Ų▀(2)░Óėą50├¹īW(xu©”)╔·Ż¼└ŽÄ¤░▓┼┼├┐╚╦ųŲū„ę╗╝■Aą═╗“Bą═Ą─╠š╦ćŲĘ����Ż¼īW(xu©”)ą�Ż¼F(xi©żn)ėą╝ūĘNųŲū„▓─┴Ž36Ū¦┐╦Ż¼ęęĘNųŲū„▓─┴Ž29Ū¦┐╦�Ż¼ųŲū„AĪóBā╔ĘNą═╠¢(h©żo)Ą─╠š╦ćŲĘė├┴ŽŪķør╚ńŽ┬▒ĒŻ║
ąĶ╝ūĘN▓─┴Ž ąĶęęĘN▓─┴Ž
1╝■Aą═╠š╦ćŲĘ 0.9Ū¦┐╦ 0.3Ū¦┐╦
1╝■Bą═╠š╦ćŲĘ 0.4Ū¦┐╦ 1Ū¦┐╦
(1)įO(sh©©)ųŲū„Bą═╠š╦ćŲĘx╝■�����Ż¼Ū¾xĄ─╚ĪųĄĘČć·;
(2)šł(q©½ng)─ŃĖ∙ō■(j©┤)īW(xu©”)ąŻ¼F(xi©żn)ėą▓─┴Ž�����Ż¼Ęųäeīæ│÷Ų▀(2)░ÓųŲū„Aą═║═Bą═╠š╦ćŲĘĄ─╝■öĄ(sh©┤)�����ĪŻ
Ęų╬÷Ż║▒ŠŅ}Ņ}─┐ųąø](m©”i)ėą│÷¼F(xi©żn)├„’@Ą─▒Ē╩Š▓╗Ą╚ĻP(gu©Īn)ŽĄĄ─ūų�Ż¼╦∙ęį▓╗Ą╚ĻP(gu©Īn)ŽĄ▒╚▌^ļ[║¼Ż¼Ęų╬÷Ņ}ęŌ┐╔░l(f©Ī)¼F(xi©żn)����Ż¼ųŲū„ā╔ĘNą═╠¢(h©żo)Ą─╠š╦ćŲĘĄ─▓─┴ŽęčĮo│÷Ž▐ųŲŻ¼╦∙ė├▓─┴Ž▓╗─▄│¼▀^(gu©░)▀@éĆ(g©©)Ž▐ųŲ�Ż¼ę“┤╦╬ęéāŠ═┐╔ęįĖ∙ō■(j©┤)┐é▓─┴ŽĄ─Ž▐ųŲüĒ(l©ói)┴ą│÷▒ŠŅ}Ą─▓╗Ą╚╩ĮĮMĪŻ
ĮŌŻ║(1)įO(sh©©)ųŲū„Bą═╠š╦ćŲĘx╝■����Ż¼ätųŲū„Aą═╠š╦ćŲĘ×ķ(50-x)╝■Ż¼ė╔Ņ}ęŌ�Ż¼Ą├

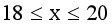
ĮŌĄ├
(2)ė╔(1)ų¬Ż¼ėųę“?y©żn)ķx×ķš¹öĄ(sh©┤)Ż¼
╦∙ęįx=18��Īó19����Īó20Ż¼50-x=32���Īó31����Īó30
╦∙ęįŲ▀(2)░ÓųŲū„Aą═║═Bą═╠š╦ćŲĘĄ─╝■öĄ(sh©┤)ėą╚²ĘN┐╔─▄Ż║
┐╔─▄ę╗Ż║ųŲū„Aą═╠š╦ć32╝■�Ż¼Bą═╠š╦ć18╝■;
┐╔─▄Č■Ż║ųŲū„Aą═╠š╦ć31╝■Ż¼Bą═╠š╦ć19╝■;
┐╔─▄╚²Ż║ųŲū„Aą═╠š╦ć30╝■�����Ż¼Bą═╠š╦ć20╝■�����ĪŻ
ĪĪĪĪ ÜgėŁ╩╣ė├╩ųÖC(j©®)�ĪóŲĮ░ÕĄ╚ęŲäė(d©░ng)įO(sh©©)éõįLå¢(w©©n)ųą┐╝ŠW(w©Żng)�Ż¼2024ųą┐╝ę╗┬Ę┼Ń░ķ═¼ąąŻĪ>>³c(di©Żn)ō¶▓ķ┐┤









