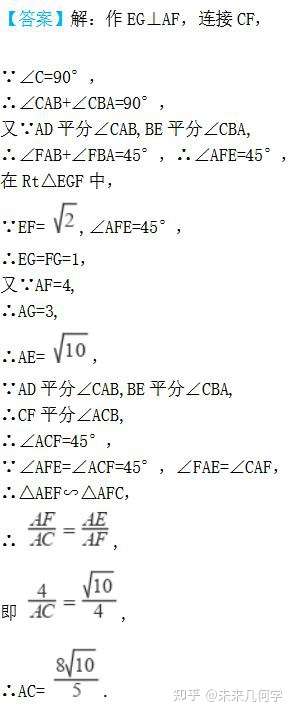≥ű÷–é◊ļő“Ľ÷Ī «≤Ľ…ŔÕ¨ĆWĪ»›^Ó^ŐŘĶńÜĖÓ}°£‘ŕ◊C√ųé◊ļőÓ}ēr�£¨’“≤Ľú ∑ĹŌÚ£¨“‘÷Ń”ŕ«ßÓ^»fĺw��£¨≤Ľ÷™Źńļő»Ž ÷;…ű÷Ń“‘«į◊ŲŖ^ĶńÓ}�����£¨“≤»ÁŖ^—Ř‘∆üü�����°£
Ŗ@ « ≤√ī‘≠“Ú?
ő“’Jěť «õ]”–’∆ő’ĒĶ(sh®ī)ĆWĆWŃēĶń∑Ĺ∑®����°£‘ŕŖ@ņÔő“Ō»ļÜÜőĶńĹťĹBŌ¬ő“◊‘ľļĶńĒĶ(sh®ī)ĆWĆWŃē«ťõr(ń„āÉ“≤Ņ…“‘ņŪĹ‚ěťő“ŖmģĒ?sh®ī)ńīĶáuŌ¬◊‘ľļ)£ļ–°ĆWļÕ≥ű÷–ĒĶ(sh®ī)ĆW√ŅīőŅľ‘á“™√ī «ĚM∑÷“™√ī «Ĺ”ĹŁĚM∑÷;łŖ÷–’żļ√”ŲĶĹő“Ķń«ŗīļŇ—ńś∆ŕ£¨ĒĶ(sh®ī)ĆW≥…ŅÉ”–ňýŌ¬Ľ¨;ĶęĶĹŃňīůĆW“‘ļů���£¨ĒĶ(sh®ī)ĆW≥…ŅÉ”÷ÕĽÔw√ÕŖM;—–ĺŅ…ķ’–…ķŅľ‘á���£¨ĒĶ(sh®ī)ĆWŅľŃň139∑÷(ĚM∑÷150£¨139‘ŕģĒńÍ’śň„Ķń…Ō «ļ‹łŖĶń∑÷ĒĶ(sh®ī)���£¨÷‹áķļ‹∂ŗ∆Ĺēr≥…ŅÉļ‹ļ√ĶńÕ¨ĆWŖB90∑÷∂ľõ]”–)Ķńļ√≥…ŅÉ;2019ńÍÖĘľ”łŖ÷–ĹŐéüŔYłŮ◊CŅľ‘á�����£¨“Ľīő–‘Õ®Ŗ^(ģĒēr”–“ĽāÄ87»ňŅľ≥űłŖ÷–ĒĶ(sh®ī)ĆWĹŐéüŔYłŮ◊CĶńőĘ–Ň»ļ�£¨ÉH»ż»ňÕ®Ŗ^�����£¨ŃŪÕ‚É…āÄÕ®Ŗ^Ķń «≥ű÷–ĹŐéüŔYłŮ◊C)£¨“™÷™ĶņŖ@Žxő“2008ńÍīT ŅģÖėI(y®®)���£¨“—Ĺõ(j®©ng)11ńÍŖ^»•Ńň��°£11ńÍõ]ŅīŖ^ĒĶ(sh®ī)ĆW��£¨“Ľīő–‘Õ®Ŗ^łŖ÷–ĒĶ(sh®ī)ĆWĹŐéüŔYłŮ◊CŅľ‘á(ļ¨≥ű÷–��°ĘłŖ÷–����°ĘīůĆWÉ»(n®®i)»›)�£¨ « ≤√īłŇńÓ? «“Úěťő“ĒĶ(sh®ī)ĆWĽýĶA‘ķĆć∑Ä(w®ßn)ĻŐ£¨11ńÍ∂ľõ]‘ű√īÕŁ”õ��°£“≤ĺÕ «’f÷Ľ“™ńķĆWŃē∑Ĺ∑®Ķ√ģĒ����£¨’ś’żņŪĹ‚ŃňĒĶ(sh®ī)ĆWłŇńÓ£¨ľī ĻŖ^‘Ŕĺ√ďž∆ūĀŪ“≤∑«≥£»›“◊�°£
ļ√£¨řDĽō’żÓ}�°£
é◊ļő≤ĽÉHÉH «≥ű÷–ĒĶ(sh®ī)ĆWĶń÷ōŁc£¨‘ŕłŖ÷–ĒĶ(sh®ī)ĆW÷–“≤’ľ”–ŌŗģĒīůĶńĪ»÷ō�£¨∆šŽy∂»≥ ¬›–ż Ĺ…Ō…ż����£¨ňý“‘≥ű÷–é◊ļőĽýĶA“Ľ∂®“™īÚļ√����°£ļ√‘ŕ≥ű÷–é◊ļő◊ÉĽĮ≤Ę≤Ľ∂ŗ���£¨īůÕ¨–°ģź����£¨÷Ľ“™’∆ő’ŃňĆWŃēĽÚňľŅľĶń∑Ĺ∑®�����£¨–°Ķń≤ÓģźŇe“Ľ∑ī»ż���£¨īů∂ŗĒĶ(sh®ī)é◊ļőÓ}Ī„”≠»–∂ÝĹ‚���°£
ĆWļ√ĒĶ(sh®ī)ĆW≤Ľ∑Ń∑÷ěť“‘Ō¬é◊≤Ĺ£¨»ÁĻŻń„ń‹◊x∂ģ≤ĘąŐ(zh®™)––���£¨90%ĶńÓ}ńŅń‹“Ľ∑÷Áä÷ģÉ»(n®®i)…ű÷Ńé◊√ŽÁä÷ģÉ»(n®®i)≥ŲĹ‚Ó}ňľ¬∑����£¨Ōŗ–Ňń„ĶńĒĶ(sh®ī)ĆW≥…ŅÉēĢ”–Ŕ|(zh®¨)ĶńÔw‹S!
Ķŕ“Ľ≤Ĺ£ļņő”õłŇńÓ°Ę∂®ņŪ����°Ę–‘Ŕ|(zh®¨)
ļ‹∂ŗľ“ťL°ĘņŌéü÷Ľ÷™Ķņ◊Ć◊‘ľļļĘ◊”ĽÚ?q®Ī)W…ķ∂ŗňĘÓ}�£¨Ćć––Ó}ļ£Ďū(zh®§n)–g£¨Ķę «ňŻāÉ≤Ľ«Ś≥Ģ◊‘ľļĶńļĘ◊”…ű÷ŃŖB’nĪĺ…ŌĶńĽýĪĺłŇńÓ∂ľŌ°ņÔļżÕŅ����°£“Ľő∂Ķń◊ŲÓ}£¨į—ļĘ◊”Ň™Ķ√…Ū–ńĺ„∆£≤Ľ’f����£¨…ű÷ŃēĢģa(ch®£n)…ķĶ÷”|«ťĺw°£ĶĹ◊Óļů“ņ»Ľ÷ĽēĢ◊Ų–©ļÜÜőĶńÓ}ńŅ����£¨Ć¶”ŕ›^ŽyĶńÓ}ńŅ£¨÷Ľ“™…‘őĘ”––©◊ÉĽĮ�����£¨“ņ»Ľ≤ĽēĢ£¨Ŗ@ė”ēĢ ĻļĘ◊”÷ūĚu ß»•Ć¶ĒĶ(sh®ī)ĆWĆWŃēĶńŇd»§��°£’fĆć‘í����£¨Ŗ@ė”Ķńľ“ťLļÕņŌéü≤Ľ‘ŕ…ŔĒĶ(sh®ī)°£
∆šĆćīů≤Ņ∑÷Ņīň∆›^ŽyĶńÓ}ńŅ∂ľ «ŹńĽýĪĺĶń∂®Ńx����°Ę∂®ņŪļÕ–‘Ŕ|(zh®¨)»Ž ÷����£¨≤Ľ–Ň?“ĽēĢŇeé◊āÄņż◊”ń„ŅīŅīĺÕ÷™ĶņŃň°£
ń«√ī»Áļő≤Ňń‹ žĺöĶń’∆ő’Ŗ@–©◊ÓĽýĪĺĶń÷™◊Rńō?ő“’Jěť–Ť“™◊Ųļ√“‘Ō¬»żŁc£ļ1��°Ę ž◊xĹŐ≤ń�����£¨ņŪĹ‚Ŗ@–©łŇńÓĶńīķĒĶ(sh®ī)ļÕé◊ļő“‚Ńx;2�°Ę žĪ≥∂®Ńx∂®ņŪ–‘Ŕ|(zh®¨)(’l’fĒĶ(sh®ī)ĆW≤Ľ”√Ī≥Ķń?Žm’f≤ĽŌŮ’Zőń”Ę’ZĪ≥Ķńń«√ī∂ŗ£¨ģĒ»Ľ≤Ľ «ňņ”õ”≤Ī≥����£¨∂Ý «‘ŕņŪĹ‚ĶńĽýĶA…Ō»•Ī≥’b);3°Ę◊ŲÓ}ĶńŖ^≥Ő÷–“™«Ś≥Ģ√Ņ“ĽÓ}Ď™”√Ńň ≤√īłŇńÓ∂®ņŪļÕ–‘Ŕ|(zh®¨)°£
»ÁĻŻń‹ņő”õ≤Ę’∆ő’łŇńÓ���°Ę∂®ņŪ��°Ę–‘Ŕ|(zh®¨)����£¨◊ŲĶĹ“‘…Ō»żŁc�����£¨ń«√īĻßŌ≤ń„���£¨ń„Ŗ_ĶĹŃňľįłŮĺÄ�£¨“≤ĺÕ «’fŅľ‘áĚM∑÷100∑÷���£¨ń„ń‹Ķ√āÄ60∑÷ «≤Ľ≥…ÜĖÓ}Ķń���°£

≥ű÷–é◊ļő
ģĒ»Ľő“āÉĹ^īů≤Ņ∑÷Õ¨ĆW≤ĽĚM◊„60∑÷ĶńľįłŮ≥…ŅÉ£¨ń«‘ű√īřk?≤ĽľĪ��£¨ő“āÉņ^ņm(x®ī)ŅīĶŕ∂Ģ≤Ĺ£ļ
Ķŕ∂Ģ≤Ĺ£ļ»Áļő»•ňľŅľ?
ļ‹∂ŗĆW…ķŇŲĶĹ›^ěťž`ĽÓĽÚ…‘”–Žy∂»ĶńÓ}ńŅ����£¨«ßÓ^»fĺw��£¨įŔňľń™Ĺ‚��°£Ŗ@∆šĆć «“Úěťõ]”–◊•◊°≥ű÷–é◊ļőĶńĪĺŔ|(zh®¨)����£¨“‘ľįňľŅľĶń∑Ĺ∑®����°£ĆćŽH…Ōļ‹∂ŗÓ}ČļłýĺÕ≤Ľ”√ń„‘ű√ī»•ňľŅľ£¨÷Ľ“™ń„’∆ő’Ńň“ĽāÄĻŐ∂®ĶńĹ‚Ó}∑Ĺ∑®�°£
ő“āÉŌ»ĀŪŃňĹ‚≥ű÷–é◊ļőĶńĪĺŔ|(zh®¨)——≥ű÷–ŽA∂őĶńīů∂ŗĒĶ(sh®ī)ĒĶ(sh®ī)ĆWé◊ļőÓ}����£¨ĪĺŔ|(zh®¨)…Ō∂ľ «Ć¶ĺÄĽÚĹ«÷ģťgÍPŌĶĶńŐéņŪ°£”õ◊°�£¨‘ŔŹä’{(di®§o)“ĽĪť£ļĺÄĽÚĹ«(ĺÄŇcĺÄ°ĘĺÄŇcĹ«�����°ĘĹ«ŇcĹ«)÷ģťgÍPŌĶĶńŐéņŪ���°£
“≤ĺÕ «’f��£¨»ÁĻŻ‘ŕĹ‚Ó}ĶńŖ^≥Ő÷–�£¨”–“‚◊RĶō»•’“ŇcólľĢĽÚĹY’ďŌŗÍPĶńĹ«ĽÚĺÄĶńÍPŌĶ£¨‘Ĺ∂ŗ‘Ĺļ√����£¨ňľ¬∑Õ®≥£ļ‹Ņž◊‘»Ľ∂Ý»ĽĺÕ≥ŲĀŪŃň°£“Ľį„«ťõrŌ¬��£¨Ĺ‚Ó}ēr–Ť“™Ō»’“≥ŲÕĽ∆∆Ņŕ�����£¨ÕĽ∆∆Ņŕ‘ŕńń?ĺÕ «Ó}ńŅ÷–ĶńÍPśI’Zĺš����°£
ļ√£¨ő“āÉĀŪŅīŌ¬√śŖ@ĶņņżÓ}£ļ
ņż1��°Ę»ÁąD�£¨‘ŕ∆Ĺ––ňńŖÖ–őABCD÷–£¨E «AB…Ō“ĽŁc�£¨DE°ĘCE∑÷Ąe «∠ADC�����°Ę∠BCDĶń∆Ĺ∑÷ĺÄ.»ŰAD=5£¨DE=6���£¨Ąt∆Ĺ––ňńŖÖ–őABCDĶń√ś∑e «()
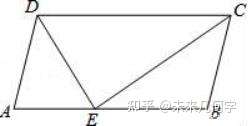
ņż1 ąD1-1
A.96 B.60 C.48 D.30
°ĺňľŅľ°ŅŖ@“ĽÓ} «◊Ćő“āÉ«ů∆Ĺ––ňńŖÖ–őABCDĶń√ś∑e���°£ő“āÉ◊Ó»›“◊ŌŽĶĹ «Ļę Ĺ∑®£ļ Ķ◊׳Ŗ;Ķŕ∂Ģ∑N∑Ĺ∑®£ļ“≤Ņ…“‘řDĽĮěťé◊āÄ»żĹ«–őĶń√ś∑eļÕ£¨∂Ý«ů»żĹ«–őĶń√ś∑eĻę Ĺ «Ķ◊׳Ŗ÷2�°£ŅīŅīŖ@É…∑N∑Ĺ∑®ĪĺŔ|(zh®¨)…Ō∂ľ «ĺÄŇcĺÄĶńÍPŌĶ����°£
ń«ő“āÉĺÕ—ō÷ÝŖ@ól÷ųĺÄřDĽĮÓ}ńŅ÷–Ķń√ŅāÄólľĢ£ļő“āÉŅīĶĹólľĢ÷–ÍPśI’Zĺš «Ĺ«∆Ĺ∑÷ĺÄ£¨ń«√īő“āÉ≤Ľ”√»•ňľŅľ�£¨÷ĪĹ”ĺÕņŻ”√Ĺ«∆Ĺ∑÷ĺÄĶń–‘Ŕ|(zh®¨)£¨į—ňý”–ŌŗĶ»ĶńĹ«ėň”õ≥ŲĀŪ��°£”–Õ¨ĆW“≤‘SēĢÜĖ���£¨ő“āÉ«ůĶń «ĺÄŇcĺÄĶńÍPŌĶ£¨ėň≥ŲŌŗĶ»ĶńĹ«”– ≤√ī”√?‘≠“Ú‘ŕ”ŕ£ļ“Ľ��°ĘÓ}ńŅ÷–◊ÓÍPśIĶń’Zĺš÷Ľ”–Ĺ«∆Ĺ∑÷ĺÄ�����£¨ő“āÉ÷Ľ”–ņŻ”√Ĺ«∆Ĺ∑÷ĺÄĶń–‘Ŕ|(zh®¨)≤Ľ «?∂Ģ°ĘĹ«ĶńÍPŌĶļ‹∂ŗērļÚ∂ľŅ…“‘řDĽĮ≥…ĺÄŇcĺÄĶńÍPŌĶį°���£¨◊Ó≥£”√ĶńĶ»—Ł»żĹ«–őÉ…—ŁŌŗĶ»≤Ľ «ÜŠ?
ļ√��£¨ņŻ”√Ĺ«∆Ĺ∑÷ĺÄĶń–‘Ŕ|(zh®¨)�£¨ő“āÉ‘ŕąD÷–ėň≥ŲEDĆĘ∠ADC∑÷ěťÉ…āÄŌŗĶ»Ķń∠1���£¨ECĆĘ∠DCB∑÷ěťÉ…āÄŌŗĶ»Ķń∠2����°£ń«√īŖ@ė”ő“āÉ «∑Ůį—ňý”–ŌŗĶ»Ķń∠1ļÕ∠2∂ľėň≥ŲĀŪŃň?Ô@»Ľ≤Ľ «!“Úěťő“āÉŅ…“‘ŅīĶĹ÷Ľėň≥ŲŖ@ɅƶŌŗĶ»ĶńĹ«õ]”–”√�£¨ŖÄ «Ĺ‚≤Ľ≥ŲĀŪ°£ń«√īő“āÉ’J’ś◊x“ĽŌ¬Ó}ńŅólľĢ���£¨įl(f®°)¨F(xi®§n)Ņ…“‘‘ŔłýďĢ(j®ī)∆Ĺ––ňńŖÖ–őɅƶŖÖ∆Ĺ––Ķń–‘Ŕ|(zh®¨)�£¨ėň≥ŲąD÷–ňý”–Ňc∠1ļÕ∠2ŌŗĶ»ĶńĹ«�����°£
ń«Ŗ@Ňc∆Ĺ––ňńŖÖ–ő√ś∑e”– ≤√īÍPŌĶńō?ő“āÉ‘ŔłýďĢ(j®ī)Ąā≤Ň«ůĶ√ŌŗĶ»ĶńĹ«řDĽĮ≥…ĺÄ∂őŇcĺÄ∂őĶńÍPŌĶ���£¨ļ‹»›“◊Ņī≥Ų°ųADEļÕ°ųBCEěťĶ»Ĺ«»żĹ«–ő����£¨ľīAD=AE=5°ĘBE=BC=5����°£Źń∂Ýņ^ņm(x®ī)«ůĶ√AB=10£¨‘ŔņŻ”√ĻīĻ…∂®ņŪĽÚ’ŖĶ»√ś∑e∑®«ůĶ√°ųADEĶńAEŖÖ…ŌĶńłŖ(“≤ěť∆Ĺ––ňńŖÖ–őĶńłŖ)�����£¨Źń∂Ý«ůĶ√∆Ĺ––ňńŖÖ–őĶń√ś∑e��£¨‘Ēľö’ąŅīĪĺÓ}Ĺ‚∑®“Ľ�����°£
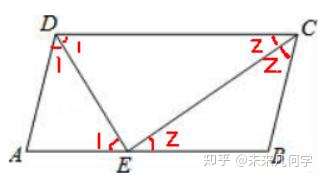
ņż1 ąD1-2
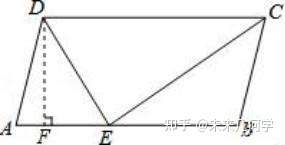
ņż1 ąD1-3
∑Ĺ∑®“Ľ£ļŖ^ŁcD◊ųDF⊥AB”ŕŁcF��£¨
°ŖDE�°ĘCE∑÷Ąe «∠ADC°Ę∠BCDĶń∆Ĺ∑÷ĺÄ���£¨ ( ◊Ō»ŹńÍPśI’ZĺšĹ«∆Ĺ∑÷ĺÄ»Ž ÷)
∴∠ADE=∠CDE�����£¨∠DCE=∠BCE�����£¨
°ŖňńŖÖ–őABCD «∆Ĺ––ňńŖÖ–ő�����£¨
∴AB°őDC�����£¨AD=BC=5���£¨
∠CDE=∠DEA£¨∠DCE=∠CEB�����£¨ (‘ŔņŻ”√∆Ĺ––ĺÄĶń–‘Ŕ|(zh®¨)���£¨’“≥Ųňý”–ŌŗĶ»ĶńĹ«)
∴∠ADE=∠AED�����£¨∠CBE=∠BEC�£¨ (Ķ»ŃŅīķďQ£¨’“≥ŲĶ»—Ł»żĹ«–ő)
∴DA=AE=5����£¨BC=BE=5£¨ (į—Ĺ«ĶńÍPŌĶřDĽĮ≥…Ĺ«ĶńÍPŌĶ)
∴AB=10����£¨
ĄtDF=DE©ĀEF=AD©ĀAF£¨
Ļ 6©ĀFE=5©Ā(5©ĀEF)����£¨
Ĺ‚Ķ√£ļEF=3.6£¨
ĄtDE==4.8�£¨
Ļ ∆Ĺ––ňńŖÖ–őABCDĶń√ś∑e «£ļ4.8×10=48.
Ļ Ŗx£ļC.
∑Ĺ∑®∂Ģ£ļģĒėň≥Ųňý”–ŌŗĶ»ĶńĹ«“‘ļůłýďĢ(j®ī)∆Ĺ––ňńŖÖ–őĶń–‘Ŕ|(zh®¨)£¨ő“āÉįl(f®°)¨F(xi®§n)∠1+∠2=90�£¨ń«√ī∠DEC=90;“ÚěťDC=AE+EB=10,DE=6£¨Ĺ‚Ķ√£ļCE=8;ňý“‘∆Ĺ––ňńŖÖ–ő√ś∑eěť2Ī∂÷ĪĹ«»żĹ«–őDECĶń√ś∑e�£¨ľī48°£
ĪĺÓ}”√ĶĹŃňĹ«∆Ĺ∑÷ĺÄ�°Ę∆Ĺ––ňńŖÖ–ő°Ę∆Ĺ––ĺÄ°ĘĶ»—Ł»żĹ«–ő�°ĘĻīĻ…∂®ņŪĶ»ĶńĽýĪĺ–‘Ŕ|(zh®¨)�����°�����£ŅīĶĹ?j®©ng)]���£¨Ŗ@ĺÕ’f√ųŃňĶŕ“Ľ≤Ĺ���£¨ ž”õ∂®Ńx°Ę∂®ņŪļÕ–‘Ŕ|(zh®¨)”–∂ŗ√ī÷ō“™!ĶęÔ@»Ľ��£¨ĪĺÓ}÷–◊Ó÷ō“™Ķń“ĽāÄólľĢ «Ĺ«∆Ĺ∑÷ĺÄ���£¨ő“āÉ…ű÷ŃŅ…“‘≤ĽĻ‹ĹY’ď“™«ů ≤√ī���£¨∂Ý÷ĪĹ””…Ĺ«∆Ĺ∑÷ĺÄĶń–‘Ŕ|(zh®¨)“żĆßėň≥Ųňý”–ŌŗĶ»ĶńĹ«°£
’∆ő’ŃňĶŕ∂Ģ≤Ĺ»Áļő»•ňľŅľ���£¨100∑÷Ķń‘áĺŪ��£¨75∑÷“‘…Ō «≤Ľ≥…ÜĖÓ}Ńň���£¨ń«»Áļő≤Ňń‹ę@»°łŁłŖ∑÷ńō?“™…∆”໕öwľ{ŅāĹY��°£
Ķ໿≤Ĺ�£¨ĆWēĢ»Áļő»•öwľ{ŅāĹY
◊ŲÕÍŃň“ĽāÄ›^ŽyĽÚ’Ŗń„’JěťĪ»›^÷ō“™ĶńÓ}ńŅēr���£¨”õĶ√»•öwľ{ŅāĹY���£¨–ő≥…◊‘ľļĶń∑Ĺ∑®ůwŌĶ°£»Áīň��£¨“‘ļů‘Ŕ”ŲĶĹÓźň∆ĶńÓ}ńŅēr�����£¨ń„Ņ…“‘ļ‹Ņž”–Ĺ‚Ó}ňľ¬∑�����°£ń«√ī‘ű√ī»•ŅāĹYöwľ{ńō?ő“āÉ≥£”√Ķń”–£ļņŪ’ď÷™◊RŁcöwľ{∑®�£¨ĺŖůwĹ‚Ó}∑Ĺ∑®öwľ{∑®����°£(◊Óļ√”–é◊āÄĺę÷¬ĶńŚeÓ}Īĺ�°£ěť ≤√ī «é◊āÄ?“ÚěťŅ…ń‹‘≠ĀŪĶńöwľ{Ī»›^ú\Ô@£¨ŽS÷ÝĆWŃēĶńŖM––ļÕ…Ó»Ž����£¨ļů√śĶńöwľ{ēĢ‘ĹĀŪ‘ĹļÜĺö��°Ę»ę√ś��°Ę…ÓŅŐ)
3.1����°ĘņŪ’ď÷™◊RŁcöwľ{∑®
ľīő“āÉ◊Ų“ĽĶņÓ}£¨Ņ…ń‹“™”√ĶĹńń–©ŌŗÍPĶń÷™◊R≤Ňń‹Ĺ‚īū≥ŲĀŪ��°£Ī»»Áé◊ļőÓ}÷–«ůĺÄ∂ő◊Ó–°÷Ķ�£¨ő“āÉĆWŖ^ĶńÍP”ŕ«ůĺÄ∂ő◊Ó–°÷ĶĶń∂®Ńx°Ę∂®ņŪĽÚ–‘Ŕ|(zh®¨)Ņ…“‘öwľ{‘ŕ“Ľ∆ū”–£ļ
1) É…Łc÷ģťgĺÄ∂ő◊Ó∂Ő;
2) ŁcĶĹ÷ĪĺÄĶńĺŗŽxīĻĺÄ∂ő◊Ó∂Ő;
3) »żĹ«–őÉ…ŖÖ÷ģ≤Ó–°”ŕĶ໿ŖÖ�£¨É…ŖÖ÷ģļÕīů”ŕĶ໿ŖÖ°£
ő“āÉ‘ŔĀŪŇeāÄņż◊”��£¨Ņī“ĽŅī���°£
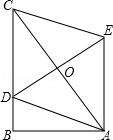
ņż2�°Ę»ÁąD£¨‘ŕRt°ųABC÷–�£¨∠B=90°£¨AB=3���£¨BC=4�����£¨ŁcD‘ŕBC…Ō�����£¨“‘ACěťĆ¶Ĺ«ĺÄĶńňý”–ADCE÷–���£¨DE◊Ó–°Ķń÷Ķ «(°°°°)
A.2 B.3 C.4 D.5
ņż2 ąD2-1
°ĺňľŅľ°ŅĹY’ď“™«ůĺÄ∂ő◊Ó–°÷Ķ£¨ń«ő“āÉńXļ£÷–ĺÕ“™ł°¨F(xi®§n)≥Ų�£¨«ůĺÄ∂ő◊Ó–°÷Ķ”–“‘…Ō»ż∑N∂®ņŪŅ…“‘Ď™”√°£ń«√īĪĺÓ}“™”√ńńāÄ∂®ņŪńō?ő“āÉņ^ņm(x®ī)∑÷őŲ£ļ
ő“āÉ’“≥ŲÓ}ńŅ÷–ĶńÍPśI’Zĺš£ļ“‘ACěťĆ¶Ĺ«ĺÄĶńňý”–ADCE÷–���°£ő“āÉ÷™Ķņ∆Ĺ––ňńŖÖ–őĶńƶūĺÄĽ•Ōŗ∆Ĺ∑÷�����£¨«ůDE◊Ó∂Ő����£¨“≤ĺÕ ««ůDO◊Ó∂Ő£¨ń«√īģĒDO ≤√īērļÚ◊Ó∂Őńō?OŁcļÕBC∂ľ «ĻŐ∂®Ķń���£¨ń«√ī÷Ľ”–ģĒOD⊥BCēr����£¨”…īĻĺÄ∂ő◊Ó∂ŐŅ…÷™��£¨īňēr����£¨DO◊Ó∂Ő�£¨“≤ľīDEĺÄ∂ő»°◊Ó–°÷Ķ.

ļ‹∂ŗÕ¨ĆWŅīĶĹĄe»ňĶńĹ‚őŲ£¨”XĶ√◊‘ľļ∂ģŃň�£¨ĺÕ»”ĶŰ≤ĽĻ‹Ńň°£≤Ľ“™“‘ěťŅīĶĹĹ‚őŲ�����£¨ń„ĺÕ’ś∂ģŃň����°£»ÁĻŻŖ@ĶņÓ}ńŅń„ť_ ľõ]◊Ų≥ŲĀŪ���£¨ĽÚ’ŖĹ‚Ó}ēr«ßÓ^»fĺw£¨Ľ®Ńňļ‹ťLērťg≤Ň◊Ų≥ŲĀŪ��£¨ń«√īŖ@āÄērļÚń„ĺÕ“™»•öwľ{Ńň�£¨į—ňŁÉ»(n®®i)ĽĮ≥…◊‘ľļĶńĖ|őų°£
‘ű√īöwľ{ńō?
◊Ō»‘ŕŚeÓ}Īĺ…ŌŃ–≥Ųé◊ļőÓ}÷–«ůĺÄ∂őĶń◊Ó–°÷Ķ����£¨ŌŗÍPĶń∂®Ńx°Ę∂®ņŪļÕ–‘Ŕ|(zh®¨)(…Ō√ś“—Ń–≥Ų���£¨īňŐé≤Ľ‘Ŕ÷ōŹÕ)»Ľļů‘Ŕį—√Ņ∑N«ťõrŌ¬√ś∂ľĆ¶Ď™ĆĎāÄé◊ĶņņżÓ}��£¨∑ĹĪ„ő“āÉŹÕŃēērƶ’’÷Ý»•ňľŅľ����°£
3.2�°ĘĺŖůw∑Ĺ∑®öwľ{∑®
ľīő“āÉ◊Ųń≥“ĽÓźÓ}£¨–Ť“™”√ĶĹ ≤√ī∑Ĺ∑®?Ī»»Áő“āÉŇŲĶĹ÷–Łc�°ĘĹ«∆Ĺ∑÷ĺÄĶ»Ķ»‘ű√ī»•◊Ų›o÷ķĺÄ?ŅīĶĹ30°Ę45�����°Ę60Őō ‚Ĺ«£¨ĽÚ’ŖŐō ‚÷Ķēr�£¨ő“āÉ ◊Ō»Ď™‘ď¬ď(li®Ęn)ŌŽĶĹ ≤√ī?ĽÚ’Ŗ ◊Ō»“™◊Ų ≤√ī?
ő“āÉ‘ŔĀŪŅī“ĽĶņÓ}£ļ
ņż3°Ę‘ŕRt°ųABC÷–�£¨∠C=90°£¨AD∆Ĺ∑÷∠CAB���£¨BE∆Ĺ∑÷∠ABC��£¨AD����°ĘBEŌŗĹĽ”ŕŁcF�£¨«“AF=4�£¨EF=£¨ĄtAC=——
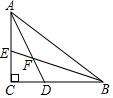
ąD ņż3-1
°ĺňľŅľ°ŅŅīĶĹÓ}ńŅ÷–”–ĺÄ∂őťLěť���£¨ő“āÉĺÕŅ…“‘“‘īňĀŪŇ–Ēŗ «∑Ů”–“‘īňĺÄ∂őěť“ĽŖÖĶńŐō ‚Ĺ«ěť45ńō?»ÁĻŻ”–����£¨ő“āÉĺÕŅ…“‘“‘īňŖÖěť÷ĪĹ«»żĹ«–őĶń–ĪŖÖėč‘ž÷ĪĹ«»żĹ«–ő���°£ő“āÉ ◊Ō»ĀŪŅīÓ}ńŅ÷–ĶńÍPśI’Zĺš£ļAD∆Ĺ∑÷∠CAB���£¨BE∆Ĺ∑÷∠ABC�£¨AD��°ĘBEŌŗĹĽ”ŕŁcF�°£”–É…ólĹ«∆Ĺ∑÷ĺÄĹĽ”ŕ“ĽŁcēr£¨≥£ŖBĹ”Ķ໿āÄŪĒŁcŇcĹ«∆Ĺ∑÷ĺÄĶńĹĽŁc;≤Ę”^≤ž»żĹ«–őÉ…Ĺ«ļÕĶń“ĽįŽ «∑ŮěťŐō ‚Ĺ«��£¨ļ‹Ô@»Ľ�£¨∠FAB+∠FBA=45°£¨ňý“‘”…Õ‚Ĺ«∂®ņŪŅ…Ķ√∠AFE=45° ���°£»Ľļů‘Ŕ“‘EFěť–ĪŖÖėč‘ž÷ĪĹ«»żĹ«–ő��£¨ľīŖ^E◊ųEGAD”ŕŁcG���°£
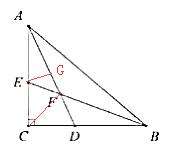
ąD ņż3-2
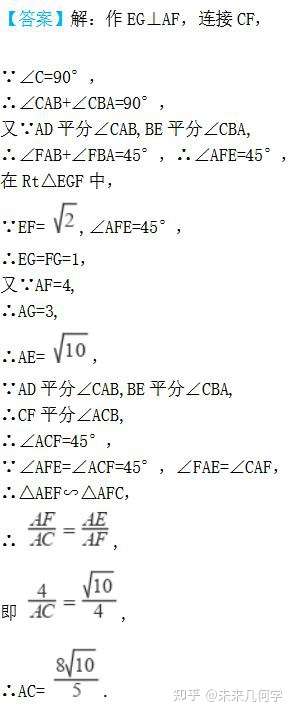
ń«√īÕ®Ŗ^Ŗ@āÄÓ}ńŅő“āÉĺÕŅ…“‘öwľ{ŅāĹY≥Ų“ĽāÄ∑Ĺ∑®£ļ
ŅīĶĹÓ}ńŅ÷–”–ĺÄ∂őťLěť°ĘĶ»Őō ‚÷Ķēr����£¨ő“āÉĺÕŅ…“‘“‘īňĀŪŇ–Ēŗ «∑Ů”–“‘īňĺÄ∂őěť“ĽŖÖĶń45°Ę60ĶńŐō ‚Ĺ«����°£»ÁĻŻ”–����£¨ő“āÉĺÕŅ…“‘“‘īňŖÖěť÷ĪĹ«»żĹ«–őĶń–ĪŖÖĽÚ÷ĪĹ«ŖÖĀŪėč‘ž÷ĪĹ«»żĹ«–ő�����°£
......
ŅīĶĹ?j®©ng)]���£¨ŅāĹY∂ŗŃň����£¨–ő≥…◊‘ľļĶń÷™◊RůwŌĶ�£¨ēr≥£úōĻ ∂Ý÷™–¬£¨Ō¬īő‘ŔŇŲĶĹŖ@ÓźÓ}ńŅ��£¨ĺÕēĢ–ő≥…ólľĢįl(f®°)…š����£¨Ō¬ĻP»Á”–…Ů!
°°°° ög”≠ Ļ”√ ÷ôC�����°Ę∆ĹįŚĶ»“∆Ą”‘Oāš‘LÜĖ÷–ŅľĺW(w®£ng)£¨2024÷–Ņľ“Ľ¬∑Ň„įťÕ¨––���£°>>ŁcďŰ≤ťŅī